크루스칼 알고리즘(Kruskal Algorithm)은 최소 신장트리 알고리즘이다.
신장트리
신장트리는 하나의 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프이다.
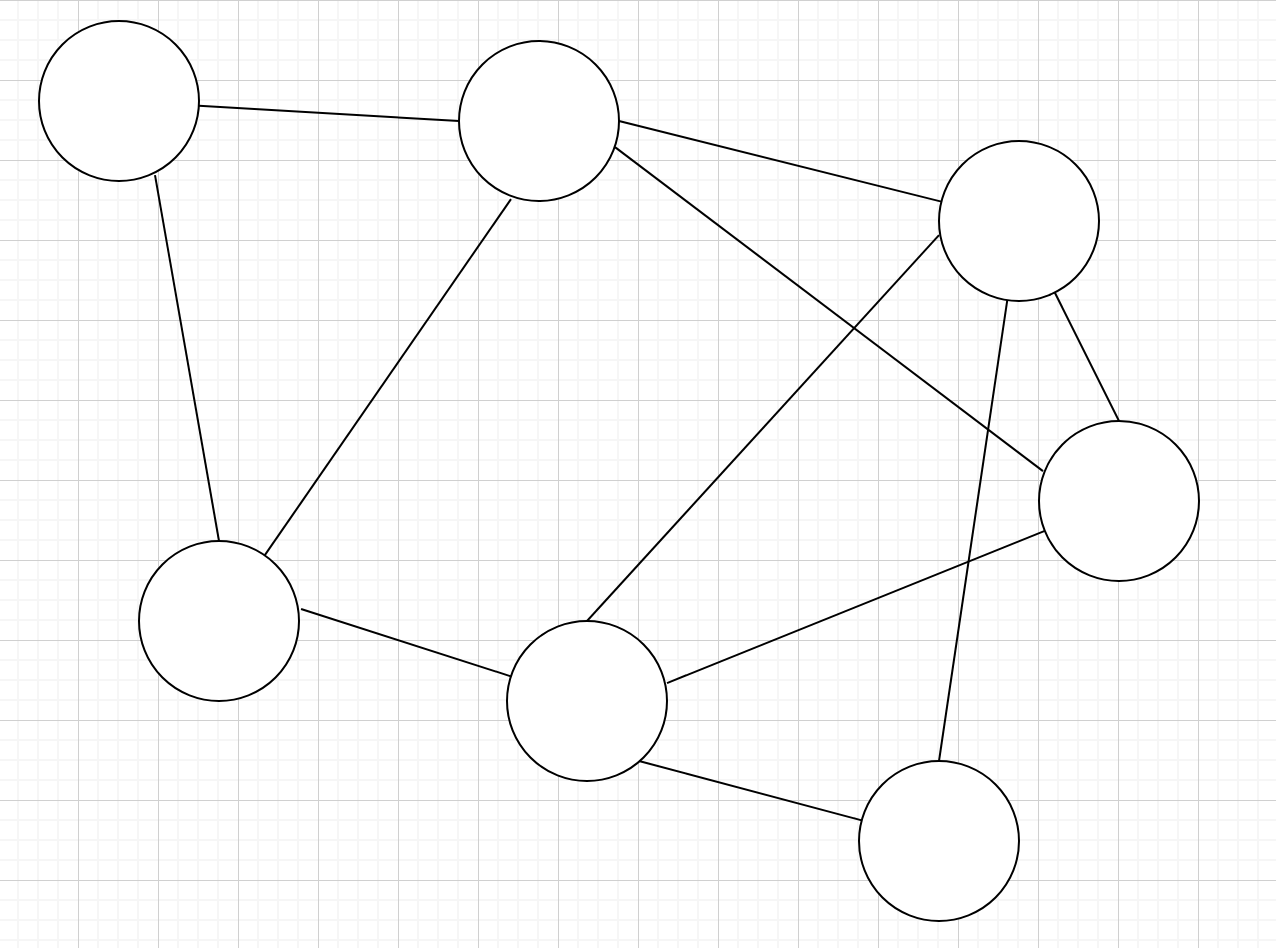
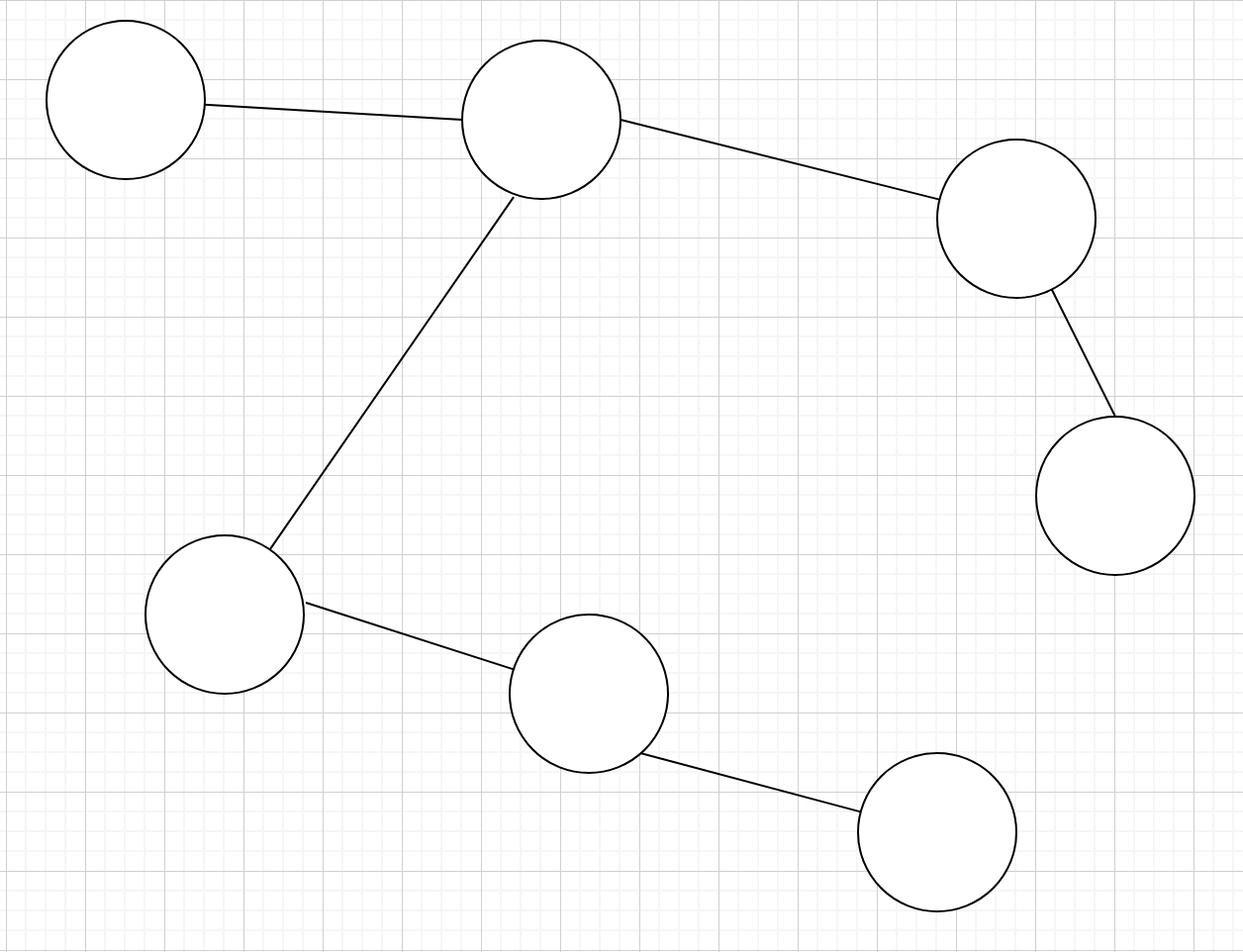
왼쪽 그래프의 신장 트리들을 찾으면 오른쪽 그래프도 그중 하나이다. 어느 노드에서 시작해도 다른 어떤 노드로 가는 방법이 있는 부분 그래프이다. 사이클이란 아래 그림의 초록색 부분이 사이클이다.

최소 신장 트리
신장 트리는 부분 그래프이기 때문에 여러 개의 경우의 수가 나온다. 최소 신장 트리는 신장 트리들 중 비용이 제일 적게 나오는 신장 트리이다. (간선들에 부여되어있는 거리 같은 비용의 총합이 제일 작은 트리) 그래서 네트워크, 인터넷 망 연결하는 알고리즘 문제에 크루스칼 알고리즘을 사용한다.
서로소 집합 자료구조
크루스칼 알고리즘을 사용하려면 서로소 집합 자료구조가 필요하다. 서로소 집합은 각 노드들의 부분 집합을 구하는 것이다.

왼쪽은 (1,2), (3,4)로 서로소 집합이 2개이고 오른쪽은 (1,2,3,4)로 서로소 집합이 1개로 이루어져 있다. (트리에서 연결되어 있는지, 즉 가는 길이 있는지 확인할 때 사용하면 좋을 듯하다.) 서로소 집합 자료구조는 union과 find 연산을 사용한다. union은 두 개의 수를 하나의 집합으로 합치는 연산(노드를 간선으로 연결한다고 생각)과 find는 부모를 찾는(union 연산을 통해 이어져 있는 1 - 2 - 3 노드가 있을 때 보통 작은 수를 부모로 판단한다. 1의 부모는 1, 2의 부모는 1, 3의 부모는 1이다.) 연산이다.
def find_parent(parent, x):
if x != parent[x]:
parent[x] = find_parent(parent, parent[x])
return parent[x]
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a > b:
parent[a] = b
else:
parent[b] = aparent 리스트에는 각자의 부모 노드를 저장한다. 처음에는 모두 본인을 본인의 노드로 세팅해둔다. (l[0]=0, l[1] = 1 ..)
a, b를 union연산을 하면 들어온 a, b의 부모를 찾는다. 그 후 a, b의 부모 중 작은 수를 부모로 설정한다.
find는 x의 부모를 찾을 때 parent리스트를 사용한다. x가 4인 경우 parent[x] = 2라면 2의 부모를 찾아서 4의 부모로 결정한다. (x != parent[x]인 경우는 x가 이미 다른 노드랑 연결되어 있어서 그래프를 더 타고 갈 수 있다는 뜻이다.)
union(4,3)를 하면 3-4가 연결되고 3과 4의 부모는 3이다. 다음으로 union(2,3)을 하면 2-3이 연결되고 2와 3의 부모는 2이다. 이런 경우 사실상 2-3-4가 모두 연결되어 있어 모든 부모는 2이다. 이렇기에 위의 코드를 모드 진행한 후 마지막으로 한번 더 find를 전체적으로 진행해 4의 parent도 2로 바꿔준다.
크루스칼 알고리즘 (Kruskal Algorithm)
크루스칼 알고리즘은 그리디 알고리즘을 사용하면서 union을 잘 사용하면 된다. 간선들을 거리(cost)가 가장 작은 순으로 정렬한다. union은 크루스칼의 조건이었던 사이클이 생기지 않는 것을 사용하면 되는데 이 부분을 a, b를 연결할 때 a, b의
부모가 같은지 아닌지를 체크한다. 부모가 같은 경우 union연산을 진행하면 사이클이 생기기 때문에 같지 않을 경우에만 union연산을 진행해 주면 된다.
Ex) 1->2, 2->3, 3->1 인 그래프가 있다. 언급한 순서대로 간선의 거리가 짧다고 가정한다. (3개의 노드가 간선으로 삼각형을 이룬다.) 이 경우 최소 신장 트리를 구하기 위해 크루스칼을 사용하면 처음에 parent 리스트는 l[1] = 1, l[2] = 2, l[3] = 3 이다.
1,2를 검사하면 부모가 다르기에 union 연산을 진행한다. 2->1 parent[2]는 1로 바뀐다.
2,3을 검사하면 부모가 다르기에 연결한다. 3->2 parent[3]은 2의 parent인 1이 된다.
마지막으로 3,1을 검사하면 l[3] = 1, l[1] = 1으로 연결 시 사이클이 발생한다. 그러므로 union연산을 하지 않는다. 즉 연결하지 않는다. cost들을 union연산을 진행한 경우 저장해 두면 최소 비용이 나온다.

'Algorithm' 카테고리의 다른 글
| 위상정렬 Topology Sort (위상 정렬 백준 문제) (0) | 2023.08.01 |
|---|---|
| 에라토스테네스의 체(소수 구하기) (0) | 2023.07.25 |
| 최단 경로 알고리즘 (다익스트라 알고리즘, 플로이드 워셜 알고리즘) (2) | 2023.07.24 |
| Defaultdict, Counter, bisect (1) | 2023.06.20 |
| 선택 정렬, 삽입 정렬, 퀵 정렬, 계수 정렬 (0) | 2023.06.19 |
