https://www.acmicpc.net/problem/1747
1747번: 소수&팰린드롬
어떤 수와 그 수의 숫자 순서를 뒤집은 수가 일치하는 수를 팰린드롬이라 부른다. 예를 들어 79,197과 324,423 등이 팰린드롬 수이다. 어떤 수 N (1 ≤ N ≤ 1,000,000)이 주어졌을 때, N보다 크거나 같고,
www.acmicpc.net
백준 문제 풀고 다른 사람들 풀이 구경하다가 소수(1과 자기 자신 외에는 나눌 수 없는 수)를 구하는 빠른 방법을 알게 되어서 작성해 본다. (전에 배웠었을 수도 있는데 일단 기억에 없다. 그러므로 정리해 두자.)
내가 사용한 방법
n이 소수인지 판별하는 방법 중 가장 우선 생각할 수 있는 쉬운 방법은 n을 반목문을 사용해 2~(n-1)로 나누어 보는 것이다. 이때 나머지가 0인 경우가 있으면 소수가 아니다. 이 방법을 사용하는데 n이 2147483647라면? 2147483645번 반복문을 돌려야 한다.(2147483647은 소수이고 1과 본인을 제외하고 나누기에 2147483645번 돌아간다.)
알고리즘 난이도가 올라갈수록 시간을 줄이는 것은 필수이기에 최적화를 해보자. 9를 소인수분해하면 1, 3, 3, 9 이다.
1 * 9 = 9, 3 * 3 =9 이다. 12를 소인수분해하면 1, 2, 3, 4, 6, 12 => 1 * 12, 2 * 6, 3 * 4. 당연히 2개의 수가 묶여서 n을 표현한다. 쉽게 말하면 2가 있기에 6이 있고 3이 있기에 4가 있다. 그러므로 앞에 수가 구해지면 뒤의 수는 당연히 존재한다. 이것을 이용해 절반만 계산하면 된다. 9를 보면 절반을 정하는 기준을 쉽게 알 수 있다. 1, 3 | 3, 9 3은 9의 제곱 근이다. 그러므로 루트 n까지만 계산을 해보면 된다. 12를 보면 1, 2, 3 | 4, 6, 12 이고 12의 제곱 근은 3.46410...이다.
정리하면 n의 제곱 근을 내림한 수까지만 계산하면 된다! 반복문이 절반만 돌아가게 된 것이다.
에라토스네스의 체
이 방법은 체로 거르듯이 수를 걸러낸다고 해서 어레토스네스의 체라고 불린다. 1 ~ 100 중에 소수를 찾아보자. 1은 예외 이므로 항상 지워둔다. 기본적인 개념은 남아있는 수는 소수라고 판별한다. 2부터 시작한다. 남아있으므로 소수로 판별한 후 2의 배수 4, 6, 8, 10, 12,, 100를 다 지운다. 2의 배수니까 당연히 2로 나누어지고 1과 본인이 아닌 수로 나누어지기에 소수가 아니다. 그다음 남아있는 수를 찾는다. 3이다. 남아있으니까 소수로 저장하고 3의 배수 6, 9, 12,,, 99를 다 지운다. 그다음 4는 2를 저장할 때 지웠고 5가 남아있다. 역시 5를 저장하고 5의 배수들을 다 지운다. 이것을 언제까지 진행해야 할까? 100의 제곱 근을 내림한 수 => 10까지만 하면 된다. 가장 큰 수가 100이니 100의 제곱 근의 배수들까지 처리하면 1 ~ 100 중 소수만 남게 된다. (지우는 것을 배열에 False로 작성하든 방법은 본인의 자유)


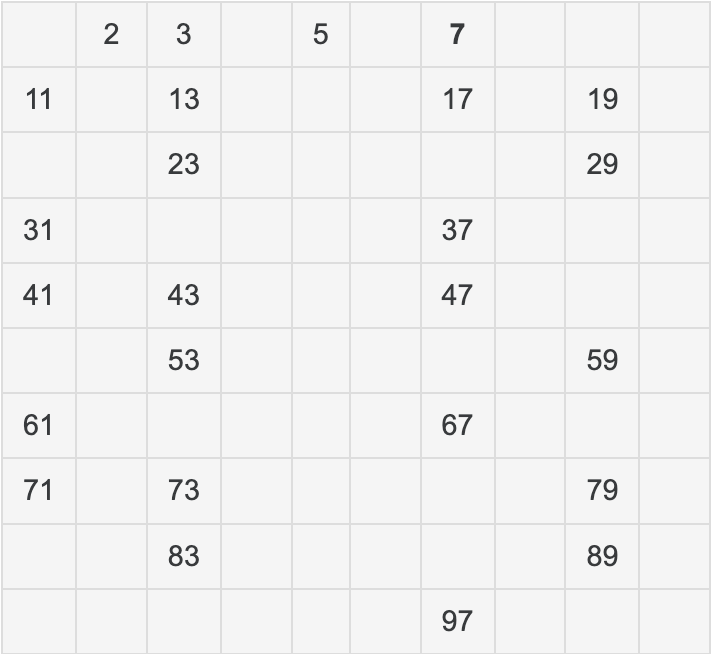
정리
1. 1을 지운다. (1은 소수도 합성수도 아니다)
2. 접근하는 수의 크기를 1 증가하며 지워지지 않은 남아있는 수를 소수로 저장하고 저장한 수의 배수는 모두 지운다.
3. 방법 2를 범위 끝 수의 제곱 근에 내림을 처리한 값까지 진행하고 멈춘다.
4. 지우지 않고 남아있는 수들이 소수이다.
'Algorithm' 카테고리의 다른 글
| 위상정렬 Topology Sort (위상 정렬 백준 문제) (0) | 2023.08.01 |
|---|---|
| 크루스칼 알고리즘 (Kruskal Algorithm, 그래프 이론, 서로소 집합 자료구조) (0) | 2023.07.30 |
| 최단 경로 알고리즘 (다익스트라 알고리즘, 플로이드 워셜 알고리즘) (2) | 2023.07.24 |
| Defaultdict, Counter, bisect (1) | 2023.06.20 |
| 선택 정렬, 삽입 정렬, 퀵 정렬, 계수 정렬 (0) | 2023.06.19 |
